25. Уравнение Бернулли

Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ?x, ?y,?z угловой скорости w.

Условием того, что движение является установившимся, является отсутствие ускорения, то есть условие равенства нулю частных производных от всех компонентов скорости:

Если теперь сложить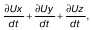

то получим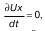

Если проецировать перемещение на бесконечно малую величину dl на координатные оси, то получим:

dx = Uxdt; dy = Uy dt; dz = Uzdt. (3)

Теперь помножим каждое уравнение (3) соответственно на dx, dy, dz, и сложим их: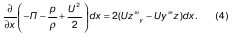

Предположив, что правая часть равна нулю, а это возможно, если вторая или третья строки равны нулю, получим:

Нами получено уравнение Бернулли