Головоломки со спичками

479. Головоломка со спичками. Взяв коробок спичек, я обнаружил, что могу составить из них любую пару правильных многоугольников, изображенных на нашем рисунке, причем на это каждый раз уходят все спички. Так, если бы у меня было 11 спичек, я мог бы из них составить, как показано, либо треугольник и пятиугольник, либо пятиугольник и шестиугольник, либо квадрат и треугольник (израсходовав на треугольник только 3 спички); но из 11 спичек нельзя составить ни треугольник с шестиугольником, ни квадрат с пятиугольником, ни квадрат с шестиугольником. Разумеется, на каждую сторону фигуры должно пойти одинаковое количество спичек.

Какое наименьшее число спичек может быть у меня в коробке?

480. Овцы и изгороди. Вот еще одна небольшая головоломка, для решения которой могут пригодиться спички. Некий фермер утверждает, что с помощью четырех жердей он может огородить квадратный участок, достаточный как раз для одной овцы. Если это и в самом деле так, то какое минимальное число жердей пойдет на загородку для десяти овец? Все зависит от формы вашей изгороди. По-другому расположить четыре спички (или жерди) вы можете только в виде ромба, и, чем более вытянутым будет этот ромб, тем меньшую площадь он будет огораживать, пока наконец после совмещения сторон огороженная площадь не обратится в нуль.

Если вы расположите шесть спичек, как в случае В, то огородите при этом участок для двух овец. Но если вы расположите их, как в случае С, то соответствующий участок подойдет только для одной овцы, поскольку овцы можно получить лишь в виде баранины. Если же вы расположите их, как в случае D, то снова в полученную загородку сможете поместить только двух овец (максимальное число в случае шести жердей).

Сколько жердей требуется для 10 овец?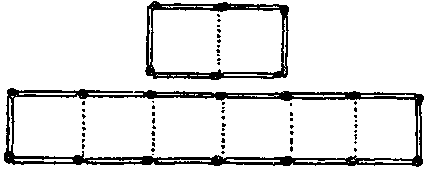

481. Двадцать спичек. На помещенном здесь рисунке показано, как можно из 20 спичек, разделенных на две группы (по 14 и 6 спичек соответственно), составить ограды для двух участков, из которых первый имеет ровно в 3 раза большую площадь, чем второй. Разделите теперь 20 спичек на две группы по 13 и 7 штук соответственно и снова огородите с их помощью два участка, у которых площадь первого была бы ровно в 3 раза больше площади второго.

482. Еще одна головоломка со спичками. Шестнадцать квадратов шахматной доски окружены 16 спичками. Требуется положить нечетное число спичек внутрь получившегося большого квадрата так, чтобы окружить 4 группы по 4 квадрата в каждой. Совершенно очевидно, как это можно сделать с помощью 8, 10 или 12 спичек, но эти числа четные.

Быть может, читателю понадобится всего лишь несколько минут для того, чтобы найти 4 различных решения (решения, переходящие друг в друга при поворотах и отражениях, не считаются различными) с нечетным числом спичек. Разумеется, не разрешается класть две спички на одну и ту же сторону.

483. Хитроумная головоломка со спичками. Положите 6 спичек, как показано на рисунке, и затем передвиньте одну из них, не касаясь остальных, так, чтобы получилась арифметическая дробь, равная 1. Спичку, изображающую горизонтальную черту дроби, трогать нельзя.

484. Нуль из пятидесяти семи. После предыдущей головоломки данная покажется совсем простой.

На нашем рисунке вы видите 6 сигарет (спички тоже вполне подойдут), которые расположены таким образом, что изображают число 57. Головоломка состоит в том, чтобы, переместив две из них и не сдвигая остальных, получить 0. Помните, что вы можете передвинуть только две сигареты. Существуют два совершенно различных решения.

Можете ли вы найти одно из них или даже оба?

485. Пять квадратов. Вот еще одна несложная головоломка со спичками, которая озадачит очень многих читателей, хотя они и рассмеются, узнав ответ.

Вы видите на рисунке, как из 12 спичек составлены 4 квадрата. Можете ли вы расположить те же 12 спичек (все спички должны лежать плашмя на столе) так, чтобы они ограничивали 5 квадратов?

Каждый квадрат должен быть «пуст», в противном случае квадраты, изображенные на рисунке, могли бы служить решением, поскольку в качестве пятого мы могли бы взять большой квадрат. Не разрешается ни укладывать две спички одна на другую, ни оставлять свободные концы.

486. Фокус со спичками. Как-то, приоткрыв спичечный коробок, я показал своим друзьям, что в нем только около дюжины спичек. Открыл я его так, что не было видно ни одной головки — все головки находились в закрытом конце коробка. Затем, закрыв коробок на глазах у всех, я сказал, что встряхну его, а потом открою снова, при этом одна спичка перевернется так, что станет видна ее головка. Так я и поступил, а зрители сразу же проверили, что все спички целы. Как мне удалось это сделать?

487. В три раза больше. Выложите на стол 20 спичек, как показано на рисунке. Можно заметить, что 2 группы из 6 и 14 спичек ограничивают 2 фигуры, площадь одной из которых ровно в 3 раза больше площади другой.

Теперь возьмите одну спичку в большой группе, переложите ее в меньшую и с помощью 7 и 13 спичек ограничьте снова 2 фигуры, из которых площадь одной была бы ровно в 3 раза больше площади другой. Двенадцать спичек должны остаться на своих местах, а кроме того, нельзя дублировать спички и оставлять свободные концы. Пунктиром отмечены соответствующие площади.

488. Фигура с шестью сторонами. Вы видите на рисунке правильный шестиугольник, составленный из 6 спичек. Можете ли вы, добавив 3 спички, изобразить с помощью 9 полученных спичек другую правильную фигуру с шестью сторонами? Не разрешается укладывать 2 спички одна на другую и оставлять свободные концы.

489. Двадцать шесть спичек. Набросайте диаграмму, подобную изображенной на нашем рисунке, где сторона каждого маленького квадрата имеет длину в одну спичку, и поместите звездочки и крестики на указанные места.

Требуется разместить 26 спичек вдоль линий таким образом, чтобы они разделяли весь чертеж на две части одинаковых размеров и одной формы, причем в одной из них должны находиться две звездочки, а в другой — два крестика.

В приведенном примере обе части, как и требуется, имеют одинаковые размеры и одну форму и в каждой из них содержатся либо две звездочки, либо два крестика, но, к сожалению, здесь использовано только 20 спичек. Следовательно, это не решение.

Можете ли вы сделать то же самое с 26 спичками?

490. Три спички. Можете ли вы расположить 3 спички на столе и на них поместить коробок так, чтобы головки спичек не касались ни стола, ни друг друга, ни коробка?

491. Равносторонние треугольники. Вот несложная головоломка для юных читателей.

Расположите 16 спичек, как показано на рисунке, чтобы они образовали 8 равносторонних треугольников. Теперь уберите 4 спички так, чтобы при этом осталось только 4 равных треугольника. Не должно оставаться ни лишних спичек, ни свободных концов.

492. Квадраты из спичек. Положите на стол 12 спичек, как показано на рисунке. Требуется переложить 6 из них так, чтобы получилось 5 квадратов. Разумеется, 6 других спичек должны остаться на месте, не разрешается дублировать спички или оставлять свободные концы.

493. Шестиугольник — в ромбы. Вот еще одна головоломка со спичками для юных читателей. Составьте шестиугольник из 6 спичек, как показано на рисунке. Сумеете ли вы теперь, передвинув всего 2 спички и добавив еще 1, получить 2 ромба?

494. Странная арифметика. Сможете ли вы показать с помощью спичек, как от 5 следует отнять , чтобы остаток оказался в точности равен 4?

495. Сосчитайте спички. Один приятель пишет, что он купил маленький коробок коротких спичек, каждая длиной дюйм. Он обнаружил, что может расположить их в виде треугольника, площадь которого содержит столько квадратных дюймов, сколько всего имеется спичек. Затем он использовал 6 спичек, и оказалось, что из оставшихся можно было составить новый треугольник, у которого площадь содержала столько квадратных дюймов, сколько оставалось спичек. А использовав еще 6 спичек, он снова сумел сделать то же самое.

Сколько спичек было у него в коробке первоначально? Это число меньше 40.